Ismerős a Fibonacci számok kifejezés? Ne aggódj, nem váltunk profilt és kezdünk matekozni és tulajdonképpen a fogalom ismerete nélkül is érthető és élvezhető a következő növények szépsége, de azért tanuljunk ma is valamit.
1202-ben egy olasz matematikus, Leonardo Fibonacci Liber Abaci című könyvében írt először erről a számsorról. Olvasta valaki? Nem? Tehát a Fibonacci számsorozat lényege a következő: az első két elem a nulla 0 és az 1, innen indulunk, ne ijedj meg. A további elemek mindig az előző kettő összegéből jönnek, azaz a 0 és az 1 után megint az 1 jön (nulla plusz egy), a következő viszont már a 2 (egy meg egy). Így néz ki: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 és így tovább. Tehát ha két számot összeadsz, abból lesz a következő, a végtelenségig. Stimt? De hogy jön ez a növényekhez?
Egyrészt a Fibonacci számsor számait megtalálhatjuk a természetben is, a virágszirmok számában: például a liliomnak, a nősziromnak és a hármassziromnak 3, a haranglábnak, a boglárkának, a larkspurnak és a vadrózsának 5, a szarkalábnak, a vérpipacsnak és a pillangóvirágnak 8 szirma van. A körömvirágnak 13, az őszirózsának 21, útilapunak 34 és így tovább. Ez már milyen izgalmas, mi?
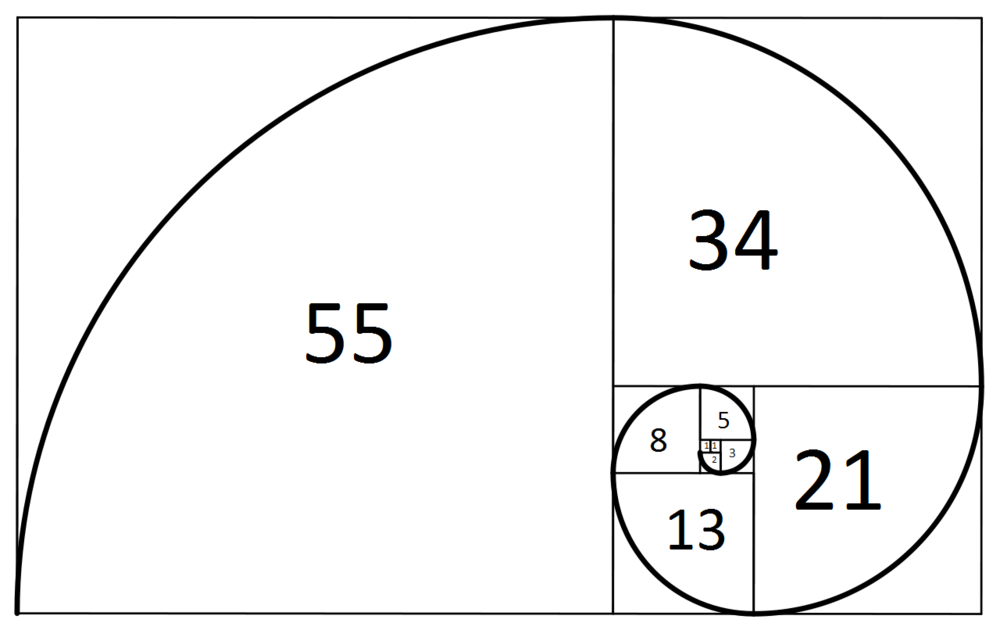
És akkor még ott van a spirál, amire a fenti galériánkban látsz példát. Ez már bonyolultabb, de a lényege, hogy a Fibonacci-spirálon egyenlő távolságra pontokat elhelyezve azok „spirálkarokká” állnak össze, és ezen karok száma Fibonacci-szám lesz. Egyes növények pedig ezek alapján Fibonacci-spirálba rendeződnek: a fenyőtoboz és az ananász pikkelyei, a napraforgó magjai, a málna szemei, a karfiol rózsái és egyes kaktuszok tüskéi és még számtalan növényé.
Forrás: wikipedia, erdekesvilag.hu, nigro.hu






